Es más o menos intuitivo que integrales del estilo $\int _{ -\infty }^{ \infty }{ f(x)dx } $ puedan calcularse en casos en las que las integrales ordinarias $\int _{ a }^{ b }{ f(x)dx } $ no pueden ser calculadas, tal es el caso de $\int _{ a }^{ b }{ { e }^{ { -x }^{ 2 } }dx } $, se demostrará el valor que tiene dicha integral, escogí esta integral por su importancia y aparte la usare en un siguiente publicación, también por que el resultado es llamativo, ya que $\pi$ vuelve a estar relacionado con $e$. Se puede resolver por varios métodos lo que haré sera cambiar de coordenadas rectangulares a polares.
$$\int _{ -\infty }^{ \infty }{ { e }^{ { -x }^{ 2 } }dx } =\sqrt { \pi }$$
Para hacer los cambios de variable se recordara la manera en la que se derivan funciones de varias variables (campos vectoriales) y se usara la matriz de jacobiana.Lo que se usara sera un cambio de variable para integrales dobles:
$$\iint _{ S }^{ }{ f(x,y)dxdy } =\iint _{ T }^{ }{ f[X(u,v),Y(u,v)]\left| J(u,v) \right| dudv } $$
De donde este factor $\left| J(u,v) \right| $ es igual al determinante de la derivada parcial de $f[X(u,v),Y(u,v)]\ $:
$$J(u,v)=\begin{vmatrix} \frac { \partial X }{ \partial u } & \frac { \partial Y }{ \partial u } \\ \frac { \partial X }{ \partial v } & \frac { \partial Y }{ \partial v } \end{vmatrix}$$
DEMOSTRACIÓN
Sea ${ S }^{ 2 }=\int _{ -\infty }^{ \infty }{ { e }^{ -x^{ 2 } }dx } \int _{ -\infty }^{ \infty }{ { e }^{ -y^{ 2 } }dy } $ como tienen diferente variable las podemos unir en una sola integral $$\int _{ -\infty }^{ \infty }{ { \int _{ -\infty }^{ \infty }{ { e }^{ -({ x }^{ 2 }+y^{ 2 }) }dx} dy } } $$Cambiaremos a coordenadas polares, tenemos que $f(x,y)={e}^{-({x}^{2}+{y}^{2})}$ nuestro cambio será $x=rcos\theta$, $y=rsen\theta$ esto es $X(r,\theta)=rcos\theta$ y $Y(r,\theta)=rsen\theta$ donde $r>0$ y $\theta$ variando de $0$ a $2\pi$ el jocobiano de este cambio de variable sera: $$J(u,v)=\begin{vmatrix} \frac { \partial X }{ \partial r } & \frac { \partial Y }{ \partial r } \\ \frac { \partial X }{ \partial \theta } & \frac { \partial Y }{ \partial \theta } \end{vmatrix}=\begin{vmatrix} cos\theta & sen\theta \\ -rsen\theta & rcos\theta \end{vmatrix}=(r\cos ^{ 2 }{ \theta } +r\sin ^{ 2 }{ \theta } )=r$$
Ya que ${ x }^{ 2 }+{ y }^{ 2 }=({ r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } )={ r }^{ 2 }$ la integral queda como: $$\int _{ 0 }^{ 2\pi }{ { \int _{ 0 }^{ \infty }{ { re }^{ -({ r }^{ 2 }) }dr } d\theta } } $$
Primero integraremos de manera normal con respecto a $r$, con un cambio de variable ${r}^{2}=u \quad 2rdr=du$ se resuelve:
$$\int _{ 0 }^{ \infty }{ { re }^{ -{ r }^{ 2 } }dr } =\frac { 1 }{ 2 } \int _{ 0 }^{ \infty }{ { e }^{ -u }du } ={ \left[ -\frac { { e }^{ -u } }{ 2 } \right] }_{ 0 }^{ \infty }=-\frac { 0 }{ 2 } +\frac { 1 }{ 2 } =\frac { 1 }{ 2 } $$
Ahora sustituyendo finalmente resolvemos:
$$\int _{ 0 }^{ 2\pi }{ { \frac { 1 }{ 2 } d\theta } } ={ \left[ \frac { \theta }{ 2 } \right] }_{ 0 }^{ 2\pi }=\frac { 2\pi }{ 2 } +\frac { 0 }{ 2 } =\pi $$
De esa manera ${S}^{2}=\pi$ pero ahora notemos que $S=\int _{ -\infty }^{ \infty }{ { e }^{ { -x }^{ 2 } }dx }$ por lo tanto se concluye que:
$$S=\int _{ -\infty }^{ \infty }{ { e }^{ { -x }^{ 2 } }dx } =\sqrt { \pi }$$
Este resultado es llamativo, ya que $\pi$ esta relacionado con el área de un circulo y en este caso por un área delimitada por el eje $x$ y la función ${e}^{-{x}^{2}}$. Mas adelante la usare para demostrar características de la función normal de densidad.
Gracias por su visita, espero sus comentarios.
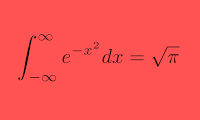
Comentarios
Publicar un comentario